Составить две программы для вычисления суммы с точностью ε, используя функцию. В одной программе реализация функции осуществить итерационным путем, в другой – через рекурсию.
Под приближенными значениями суммы наряду с точностью ε здесь понимается сумма слагаемых, для которых выполняется условие ε .
ВАРИАНТЫ, ПОД ШАБЛОН-УСЛОВИЕ:
УСЛОВИЕ: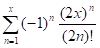
x=0.34 E=0.0001
ВЫПОЛНЕНИЕ (КОД) ДЛЯ ЭТОЙ ЗАДАЧИ В НЕСКОЛЬКИХ ВАРИАНТАХ:
МОЁ СОБСТВЕННО УСЛОВИЕ: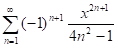
где, x=0.001 E=0.58
поправка*: желательно по такому же примерно шаблону эти задачки. Так скажем, *похоже*, но естественно можно писать как удобней. Главное - результат.
Под приближенными значениями суммы наряду с точностью ε здесь понимается сумма слагаемых, для которых выполняется условие ε .
ВАРИАНТЫ, ПОД ШАБЛОН-УСЛОВИЕ:
УСЛОВИЕ:
x=0.34 E=0.0001ВЫПОЛНЕНИЕ (КОД) ДЛЯ ЭТОЙ ЗАДАЧИ В НЕСКОЛЬКИХ ВАРИАНТАХ:
Python:
#Вариант выполения ПЕРВЫЙ:
import math
def factorial_iterative(num:int):
factorial = 1
if num < 0:
return 0
else:
for i in range (1, num + 1):
factorial = factorial*i
return factorial
x= float(input('x: '))
eps=float(input('eps:'))
n=1
sum=0
a=(-1)**n*(2*x)/factorial_iterative(2*n)
while math.fabs(a)>eps:
sum+=a
n+=1
a=(-1)**n*(2*x)**n/factorial_iterative(2*n)
print ("suma=",sum)
print("n=",n)
#ВТОРОЙ ВАРИАНТ ВЫПОЛЕНИЯ ЭТОЙ ЖЕ ЗАДАЧИ:
import math
def factorial_recursive(n):
if n == 1:
return n
else:
return n*factorial_recursive(n-1)
x= float(input('x: '))
eps=float(input('eps:'))
n=1
sum=0
a=(-1)**n*(2*x)/factorial_recursive(2*n)
while math.fabs(a)>eps:
sum+=a
n+=1
a=(-1)**n*(2*x)**n/factorial_recursive(2*n)
print ("suma=",sum)
print("n=",n)
# ТРЕТИЙ ВАРИАНТ ВЫПОЛЕНИЯ:
import math
x= float(input('x: '))
eps=float(input('eps:'))
n=1
sum=0
a=(-1)*(2*x)/(2*n)
while math.fabs(a)>eps:
sum+=a
n+=1
a=-a*(2*x)/(2*n)/(2*n-1)
print ("suma=",sum)
print("n=",n)МОЁ СОБСТВЕННО УСЛОВИЕ:
где, x=0.001 E=0.58поправка*: желательно по такому же примерно шаблону эти задачки. Так скажем, *похоже*, но естественно можно писать как удобней. Главное - результат.
