Нужна помощь в построении графика

[vladiminsk]

Нужно вычисление расстояния частицы
от начального положения,
согласно теории среднее расстояние должно быть пропорциональным времени.

Скажем для рис посчитаете для n-го шага r_n=sqrt(x_n^2+y_n^2) 25 графиков,
найдите среднее, затем для 2n-го шага повторите расчет, 3n-го шага повторите и т.д.
затем постройте график r_n=sqrt(x_n^2+y_n^2) от n.

from math import sqrt
from scipy.stats import norm
import numpy as np
 
def brownian(x0, n, dt, delta, out=None):
    """
x0 : float or numpy array 
n : int
        Количество шагов, которые нужно сделать.
dt : float
    Шаг по времени
delta : float
   дельта определяет «скорость» броуновского движения.
out : numpy array or None
     Если `out` не равно None, он указывает массив, в который следует поместить
     результат. Если `out` равно None, создается и возвращается новый массив numpy.
    """
    x0 = np.asarray(x0)
 
    # Для каждого элемента x0 генерируем выборку из n чисел из
     # нормальное распределение.
    r = norm.rvs(size=x0.shape + (n,), scale=delta*sqrt(dt))
 
    # Если `out` не был задан, создайте выходной массив.
    if out is None:
        out = np.empty(r.shape)
 
    # Это вычисляет броуновское движение, формируя кумулятивную сумму
    # случайные выборки.
    np.cumsum(r, axis=-1, out=out)
 
    # добавляем начальное условие.
    out += np.expand_dims(x0, axis=-1)
 
    return out
 
import numpy
from pylab import plot, show, grid, axis, xlabel, ylabel, title
 
# Параметр винеровского процесса.
delta = 0.30
# Общее время.
T = 10.0
# Количество шагов.
N = 500
# Размер шага по времени
dt = T/N
# Начальные значения x.
x = numpy.empty((2,N+1))
x[:, 0] = 0.0
 
brownian(x[:,0], N, dt, delta, out=x[:,1:])
 
# Постройте двухмерную траекторию.
plot(x[0],x[1])
 
# Отмечаем начальную и конечную точки.
plot(x[0,0],x[1,0], 'go')
plot(x[0,-1], x[1,-1], 'ro')
 
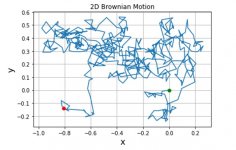
title('2D Brownian Motion')
xlabel('x', fontsize=16)
ylabel('y', fontsize=16)
axis('equal')
grid(True)
show()

 

[regnor]

я бы не рискнул качать архив...